高斯滤波
1.高斯卷积核是如何在高斯函数上取值的?
一维高斯函数的公式:
二维高斯分布的公式:
卷积核每个位置的权重值,就取对应位置对应的二维高斯函数值
,如下表
| f(-1,-1) | f(-1,0) | f(1,0) |
| f(0,,-1) | f(0,0) | f(0,1) |
| f(1,-1) | f(1,0) | f(1,1) |
卷积核的取值
#2.高斯滤波的计算公式
#
#(其中, 是归一化系数,保证高斯核中的权重值之和等于1,1)
2.为什么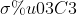 的取值会决定了高斯核半径的大小(二者知道一个另一个就随之固定)?
的取值会决定了高斯核半径的大小(二者知道一个另一个就随之固定)?
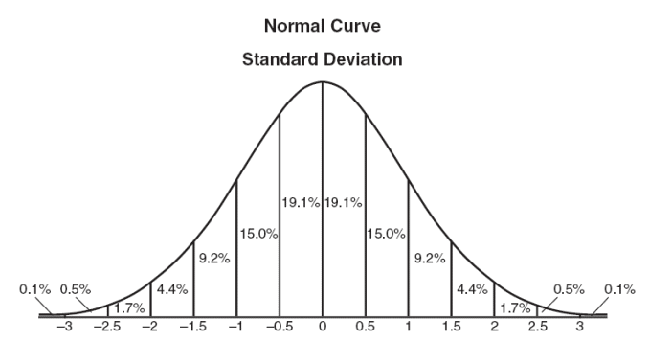
因为高斯函数的3原则(x取值在[-3
, 3
]之间的概率大于90%),根据高斯函数的图像可以看出,σ的值越大高斯函数的曲线越“平坦”(红黄蓝曲线),以一维高斯函数图像为例:

而我们知道,高斯核各个位置的权重=像素点的位置坐标对应到二维高斯函数上的函数值
当的值较小的时候(如0.2),从上面的图像可以看到
:
当x<-1、x>1的时候,f(x)的取值已经趋近于0了,这就代表着更远位置的像素值已经对计算当前位置的像素没有意义了,即小就等价于高斯核半径小。
3. 高斯滤波为什么会让图像变模糊?
高斯滤波通过高斯核对图像的逐个像素进行卷积,从而得到每个像素的值。在卷积的过程中,利用周围像素的值,将距离作为权重计算卷积核中心位置的像素。(离中心位置越近的点对像素值计算的贡献越大,选用高斯函数的原因就是因为它恰好满足这一条件)
高斯滤波是一种低通滤波,也可以说是一种数据平滑算法。“模糊”可以理解成每一个像素都取周边像素的平均值,在数值上这是一种“平滑化”,在图像上就表现出“模糊”的效果,中间点失去细节。
模糊半径越大,模糊效果越明显。考虑到图像中像素点越靠近的点关系越密切,因此加权平均是更加合理的选择。而正态分布(高斯函数)显然是一种可取的权重分配模式。
权重矩阵中所有点的权重和为1(不为1也可以吧?会使整体变暗\亮)