原始链接附带代码 :https://github.com/shl666/UCSD_CV_Intro/blob/master/chapter_2/corner_detector_matching.md
也欢迎关注我的不知道什么时候会更新的CV入门教程(根据UCSD CSE252系列课程改编):https://github.com/shl666/UCSD_CV_Intro
以下定义来自维基百科 :
特征点检测,是计算机视觉系统中用来提取特征以及推测图像内容的一种方法.角检测的应用很广,经常用在运动检测,跟踪,图像镶嵌(image mosaicing),全景图缝合(panorama stiching),三维建模以及物体识别中.
以下定义来自百度百科 :
图像处理中,特征点指的是图像灰度值发生剧烈变化的点或者在图像边缘上曲率较大的点(即两个边缘的交点)。图像特征点在基于特征点的图像匹配算法中有着十分重要的作用。图像特征点能够反映图像本质特征,能够标识图像中目标物体。通过特征点的匹配能够完成图像的匹配。
简单来说,特征点就是图像中具有代表性和鲁棒性的点,可以是角,也可以是局部亮点,抑或是线段终点。根据检测算法的不同,我们得到的特征点也有着区别。
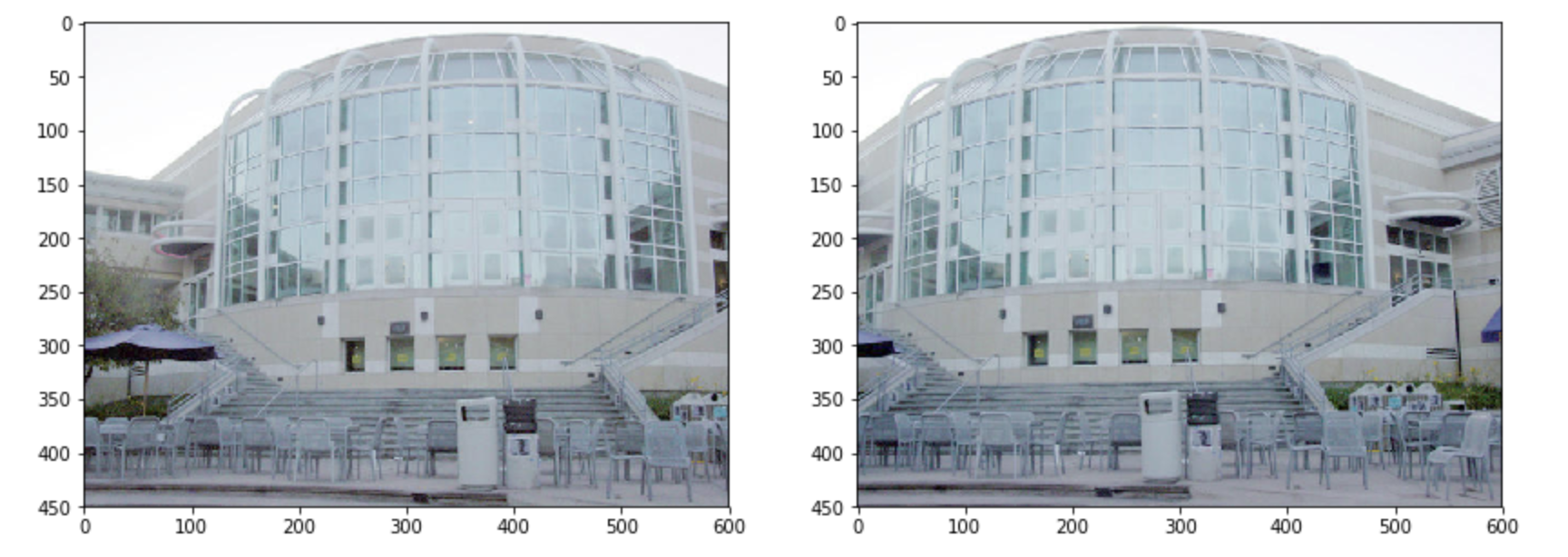
先看一下下面这两张图片(UCSD的PC):
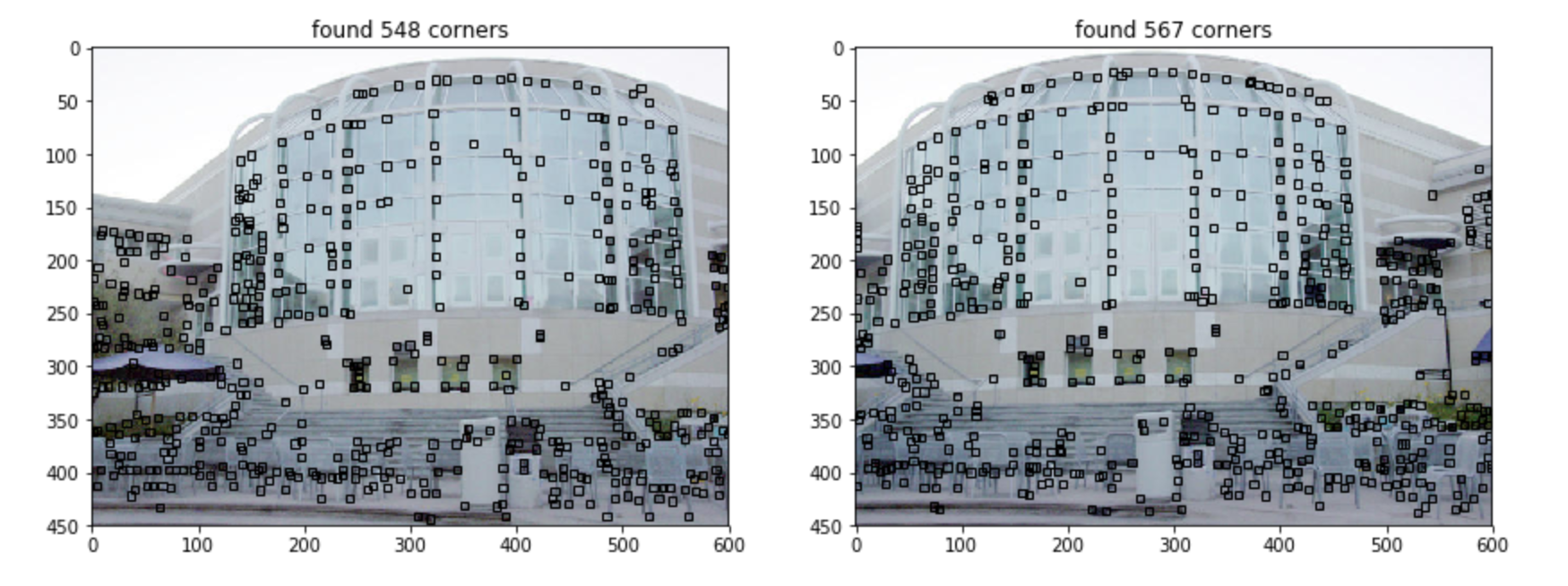
两张图片区别不大,(几乎)同一时间使用同一相机在不同角度拍下。 我们再来看看他们使用Forstner corner detection算法获得的特征点:
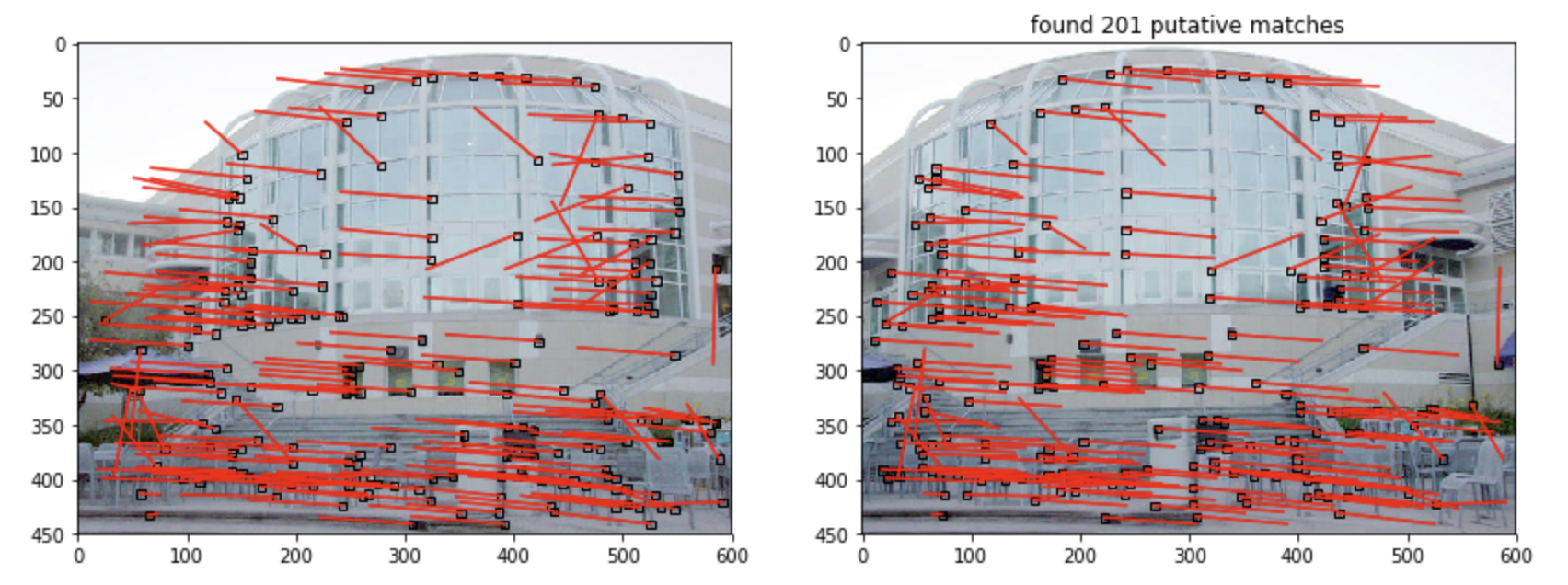
是不是几乎都是一致的?除了个别被覆盖的部分。接下来就是对这些特征点的匹配(matching)操作。
这样的matching结果,我们基本上可以看出两张图之间的变换关系了。之后利用这些关系,我们可以进行更多的应用操作。比如之前定义中提到的全景图缝合等。
好了,我们开始理一理整个算法是怎么样一个东西。
我们会有一张图片
I
I
I
然后我们需要对图片进行梯度计算,分别是横向(x轴)与纵向(y轴)。这里需要引入Five Point Central Opertor(没找到中文翻译…)。其实说到底就是一个卷积核,是根据某些数学运算推导出来的。有兴趣看深入了解的同学请点这里 。
k
x
=
1
12
[
−
1
8
0
−
8
1
]
k_x=\frac{1}{12} \left[ \begin{matrix} -1 & 8 & 0 & -8 & 1 \end{matrix} \right]
k x = 1 2 1 [ − 1 8 0 − 8 1 ]
k
y
=
1
12
[
−
1
8
0
−
8
1
]
T
k_y=\frac{1}{12} \left[ \begin{matrix} -1 & 8 & 0 & -8 & 1 \end{matrix} \right]^{T}
k y = 1 2 1 [ − 1 8 0 − 8 1 ] T
I
x
I_x
I x
I
y
I_y
I y
I
x
x
I_xx
I x x
I
y
y
I_yy
I y y
I
x
I_x
I x
I
y
I_y
I y
I
x
x
(
i
,
j
)
=
I
x
2
(
i
,
j
)
I_xx(i,j) = I_{x}^{2}(i,j)
I x x ( i , j ) = I x 2 ( i , j )
这里我们要引入下一个参数
w
w
w
N
(
i
,
j
)
=
[
∑
w
I
x
2
(
i
,
j
)
∑
w
I
x
(
i
,
j
)
I
y
(
i
,
j
)
∑
w
I
x
(
i
,
j
)
I
y
(
i
,
j
)
∑
w
I
y
2
(
i
,
j
)
]
N(i,j) = \left[ \begin{matrix} \sum_{w}{I_x^2(i,j)} & \sum_{w}{I_x(i,j)I_y(i,j)} \\ \sum_{w}{I_x(i,j)I_y(i,j)}& \sum_{w}{I_y^2(i,j)} \end{matrix} \right]
N ( i , j ) = [ ∑ w I x 2 ( i , j ) ∑ w I x ( i , j ) I y ( i , j ) ∑ w I x ( i , j ) I y ( i , j ) ∑ w I y 2 ( i , j ) ]
λ
m
i
n
(
i
,
j
)
=
T
r
(
N
(
i
,
j
)
)
−
T
r
2
(
N
(
i
,
j
)
−
d
e
t
(
N
(
i
,
j
)
)
2
\lambda_{min}(i,j) = \frac{Tr(N(i,j)) - \sqrt{Tr^2(N(i,j) - det(N(i,j))}}{2}
λ m i n ( i , j ) = 2 T r ( N ( i , j ) ) − T r 2 ( N ( i , j ) − d e t ( N ( i , j ) )
T
r
Tr
T r 迹 ,
d
e
t
det
d e t 行列式 。
再者,我们需要将图片过一个非极大抑制(NMS) 滤波器。所谓非极大抑制呢,就是在给定区域(
w
n
m
s
w_{nms}
w n m s
J
(
i
,
j
)
=
{
0
if
I
(
i
,
j
)
<
I
m
a
x
(
i
′
,
j
′
)
I
(
i
,
j
)
if
I
(
i
,
j
)
=
I
m
a
x
(
i
′
,
j
′
)
J(i,j)= \begin{cases} 0 & \text{if } I(i,j)<I_{max}(i',j')\\ I(i,j) & \text{if } I(i,j)=I_{max}(i',j')\\ \end{cases}
J ( i , j ) = { 0 I ( i , j ) if I ( i , j ) < I m a x ( i ′ , j ′ ) if I ( i , j ) = I m a x ( i ′ , j ′ )
最后一步很关键,需要引入Forstner Corner Detection算法 计算实际corner与我们筛选出来的理论corner的相对位置关系。看起来很复杂,其实只需要解一个矩阵方程即可
[
∑
w
I
x
2
(
i
,
j
)
∑
w
I
x
(
i
,
j
)
I
y
(
i
,
j
)
∑
w
I
x
(
i
,
j
)
I
y
(
i
,
j
)
∑
w
I
y
2
(
i
,
j
)
]
[
x
c
o
r
n
e
r
y
c
o
r
n
e
r
]
=
[
∑
w
x
I
x
2
(
i
,
j
)
+
y
I
x
(
i
,
j
)
I
y
(
i
,
j
)
∑
w
x
I
x
(
i
,
j
)
I
y
(
i
,
j
)
+
y
I
y
2
(
i
,
j
)
]
\left[ \begin{matrix} \sum_{w}{I_x^2(i,j)} & \sum_{w}{I_x(i,j)I_y(i,j)} \\ \sum_{w}{I_x(i,j)I_y(i,j)}& \sum_{w}{I_y^2(i,j)} \end{matrix} \right] \left[ \begin{matrix} x_{corner} \\ y_{corner} \end{matrix} \right] = \left[ \begin{matrix} \sum_{w}{xI_x^2(i,j)+yI_x(i,j)I_y(i,j)} \\ \sum_{w}{xI_x(i,j)I_y(i,j)+yI_y^2(i,j)} \end{matrix} \right]
[ ∑ w I x 2 ( i , j ) ∑ w I x ( i , j ) I y ( i , j ) ∑ w I x ( i , j ) I y ( i , j ) ∑ w I y 2 ( i , j ) ] [ x c o r n e r y c o r n e r ] = [ ∑ w x I x 2 ( i , j ) + y I x ( i , j ) I y ( i , j ) ∑ w x I x ( i , j ) I y ( i , j ) + y I y 2 ( i , j ) ]