“一天搞懂深度学习”笔记

“一天搞懂深度学习”笔记

1. A brief Introduction of Deep Learning

1.1 Introduction of Deep Learning

  • Neuron
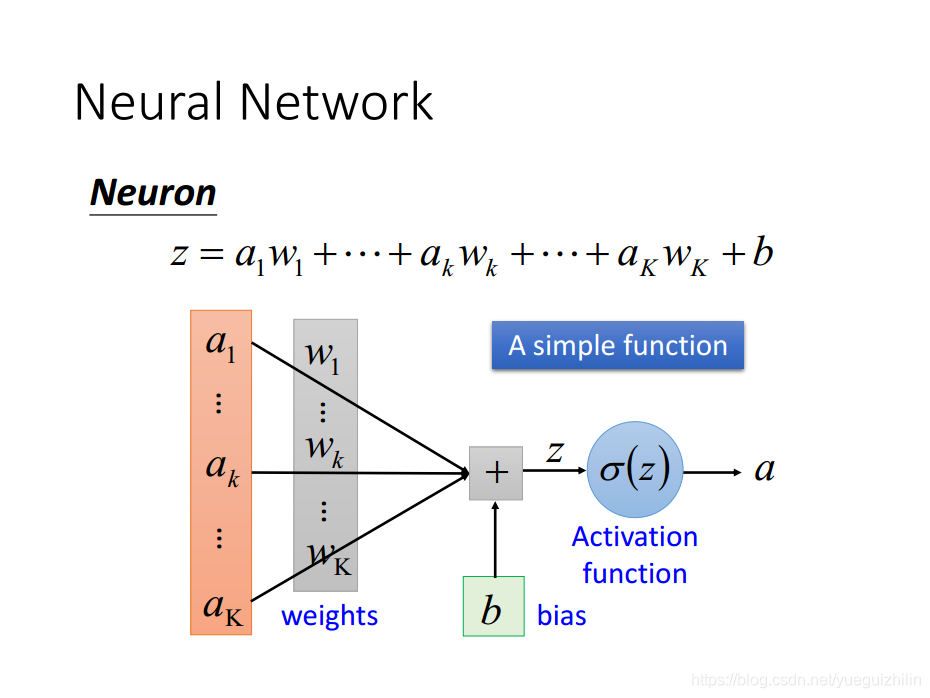
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190109113921652.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3l1ZWd1aXpoaWxpbg==,size_16,color_FFFFFF,t_70)

权重和偏置称为神经元的参数，区别于神经网络结构参数，如神经元个数，隐含层层数，网络连接方式等，网络结构参数是超参之一, 需要人为根据经验设置。

  • 全连接前馈神经网络

深度意味神经网络具有多个隐含层。

神经网络结构确定了一个函数集（函数空间），特定的神经元参数确定了函数集中一个函数。

  • soft max 输出层

softmax 输出层将网络输出值归一化到[0,1), softmax 层的输出可解释成输入vector 属于不同类的概率值。

  • loss function

loss 可以衡量网络输出和期望输出的距离。在网络结构超参确定的情况下，我们的目标就是寻找一个使loss最小的函数，最终目标转化为：通过训练数据，以最小化 loss 函数为目标，寻找最佳神经元参数。

  • 网络优化算法：寻找最佳神经元参数

基于梯度下降法的BP算法

1.2 why deep ?

实验证明，网络参数的增多，网络性能提升。

任何复杂函数均能由单隐含层的网络拟合出来。

网络参数的增多可以通过“广度学习”和“深度学习”的方式实现，哪一种方式更好呢？

在编程中，我门通过定义子函数，实现复杂函数模块化，模块化的好处是子模块实现简单、子模块可以共用、高层调度实现复杂功能且形式简洁高效（main 函数形式通常是elegant的）.类似的，我们说深度学习实现了模块化Modularization

假设我们有一个图像分类任务，若按照上图方式训练各个分类器，则因为长发男数据较少，则 Classifier 2 的性能就较为 weak.

若我们先训练两个基分类器，则两个基分类器因为有足够数据，可以训练得相当好。然后将它们视作module，第二层的每个分类器只需去 call 第一层的两个共用 modules 的 output ,就可以实现每个分类器的任务。所以虽然长头发男生的数据依然较少，此时 Classifier 2 的性能却比较 strong.

在 Deep learnin 中，第一层的每个神经元是最 basic 的 classifier ，第二层 将第一层的 classifier 当做 module 去实现复杂的 classifier ,以此类推。
故 deep learning 的好处是： 实现模组化后，每个模块会变得简单，所需训练数据较少。(这与人们津津乐谈的 AI = 深度学习+人工智能 的说法不同)

关于why deep 的直观实例，可以参看油管上一个很好的视频：
But what is a Neural Network? | Chapter 1, deep learning

2.Tips for Training Deep Neural Network

当我们训练两个分别为56层和20层的网络时，在测试集上的表现如右图所示，我门无法根据 20-layer 的损失曲线在 56-layer 的下方 ，就得出56-layer 的网络已经过拟合了。因为观察左图两者在训练集上的损失曲线，我们发现，56 layer 的网络性能居然弱于 20-layer, 这是不合理的，因为我们只要将56- layer 的网络前20 层参数与 20-layer保持一致，则损失曲线便与20-layer identity . 所以根据在训练集上的损失曲线表现看，我们对56-layer 的网络训练得还不够好，可能落入了局部最优。

所以我们得根据网络在训练集上的表现和在测试集上的表现，对症下药。例如drop out 就是针对网络在测试集上的表现较差使用的技术。


2.1 train set: choosing proper loss


当我们使用softmax输出层时，我们倾向于使用交叉熵损失函数。原因是：相较平方损失函数，交叉熵损失函数的地貌更加陡峭，梯度更大，更不容易陷入局部最优。



[图片上传中...(image.png-60b999-1518163976905-0)]

2.2 train set: Mini-batch


若batchsize 为1，就成为了随机梯度下降。
但我们一般不将batchsize 设为1.从上面PPT 可以看出，在使用GPU 进行并行运算后，在相同时间内，batchsize = 1和batchsize =10，参数的更新总次数是相近的，但是batchsize = 10 时更稳定，收敛地更快。
当batchsize 过大时，则一方面超出了GPU硬件并行能力，另一方面，此时去train 网络时会经常进入鞍点或局部极小值而无法逃离，训练过程中止，performance 下降，所以引入随机性是必要的，有助于逃离局部最优和鞍点。


2.3 train set: New activation function



  • ReLU

使用ReLU的好处是：
计算快速，激活机制与生理类似，相当于无穷多个加权sigmoid函数加权，可以防止梯度消失。


使用ReLU后，网络变成轻量的线性网络，并且这个线性网络随着输入input的不同而不同，相当于用多个线性网络去逼近一个复杂网络

  • Maxout
    Maxout 方法认为每个神经元的激活函数是可以学习的

在maxout 的隐层中的一个神经元（图中的红色框）需要比普通网络的神经元多学习一倍参数，或者多倍（取决于在一个group 中的元素个数，一个group 中的元素个数人为指定）

上图指出，ReLU是maxout学习到的激活函数中的一个特例, 即在Maxout 中学习到的参数为w,b,0,0时，则此时神经元的激活函数就等于ReLU。

学习到一个神经元的参数都非零时，则激活函数为上图形式。

maxout 可以学习到的激活函数为任意的分段线性凸函数，分段数目取决于一个group中的elementshumu


与ReLU一样，给定一个input，网络将变成一个线性网络，并且这个线性网络随着input的不同而改变。给定一个input，我们可以对这个线性网络进行训练，更新部分参数，再给定一个input，我们可以对产生的另一个线性网络进行训练，更新部分参数。所以虽然max操作不好求导，但是采用maxout的网络仍然是可以train 的。

2.4 train set: Adaptive Learning Rate

  • Adagrad
  • RMSprop

与Adagrad 只有略微的不同，RMSprop对过去梯度平方和做了加权衰减。

  • Momentum


  • Adam

2.6 test set: early stopping

early stopping其实是在控制epochs的大小

2.7 test set : Regularization





在神经网络优化中，正则项技术其实与early stopping 的功能是近似重叠的。考虑网络参数初始化为接近零的值，随着更新次数的增加，参数会越来越偏离0。所以如果参数更新次数较小，参数偏离0的程度下降，而early stopping 就是为了控制epochs 的大小。正则化技术目的也是希望参数越接近零越好。所以说两者的功能是近似的。

2.8 test set: Dropout



dripout 有效性的解释：






3.Variants of Neural Network

3.1 Convolutional Neural Network (CNN)

3.2 Recurrent Neural Network (RNN)

4.Next Wave

4.1Supervised Learning

4.1.1 Ultra Deep Network
4.1.2 Attention Model


4.2 Reinforcement Learning

4.3 Unsupervised Learning

4.3.1 Image: Realizing what the World Looks Like
4.3.2 Text: Understanding the Meaning of Words
4.3.3 Audio: Learning human language without supervision

参考资料

一天搞懂深度学习

      </div>
    </div>
</div>

更多精彩内容