这次的题目是一个简单的动态规划题。

题目：有一个小偷，计划偷窃沿街的房屋，但是不能偷两个相邻的房屋，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个数组，数组里的每个数值代表每个房屋里的财物价值，计算不触发警报的情况下能够偷窃到的最高金额。

例：

输入: [1, 2, 4, 1]
输出: 5
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 4)

输入: [3, 7, 9, 3, 2]
输出: 14
解释: 偷窃 1 号房屋 (金额 = 3), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 2)。
偷窃到的最高金额 = 3 + 9 + 2 = 14

分析：

按照动态规划的思想，我们循序渐近地分析一下哈。

假设只有一间房屋，那显然偷得的最大值就是这间屋子里的财物。假设有两个间房屋呢，那显然偷得的最大值就是这两个屋子里的金额相比较大的那个。

咦，怎么感觉so easy?! 别急，下面的才是动态规划的精髓（难点）。

先来假设一个变量：dp[i], 表示有i间屋子的情况下能偷到的最大金额。
根据以上的分析，我们很容易得知dp[1]，dp[2]。
那如果有三间屋子，有四间屋子，以至于有i间屋子，这接下去又该怎么求呢？

动态规划的重点就在于解析出状态转移方程，说人话，就是在已知dp[i-1]的情况下，怎么求dp[i]。那这里就可得细细寻思一番啦。
现在多了第i这间屋子，假设其中有金额v(i)显然，只有两种情况，要么偷，要么不偷。
那这间屋子偷与不偷取决于什么呢？很显然，取决于第i-1间屋子有没有被偷。
那么现在分析来讨论这dp[i]两种侯选情况，用dp[i]'表示：

• 第i间屋子没有被偷，那说明现在的情况是对于i-2间屋子的可偷得的最大金额再加上第i间屋子的金额，dp[i]’ = dp[i-2]+v(i)
• 第i间屋子被偷，那我们就不能偷第i+1间屋子了，即dp[i]’ = dp[i-1]

综合两种情况，即有 dp[i]=max(dp[i-2]+v(i), dp[i-1])

python代码实现：

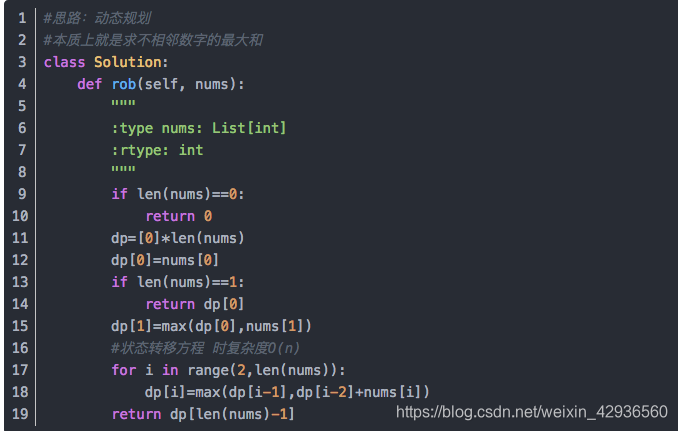
很多人卡住的地方就在于不知道这个状态转移过程应该怎么来分析。其实这道题的状态转移过程算是最简单的一种类型，只需要考虑到两种情况。

关键一点是，我们需要清楚地明白dp[i]这个符号到底代表什么，它和前面的dp[i-1]又有怎样的关系。

这种思想和中学数学中，老师给出一列数，让我们求这个数组是一样的原理，核心就是求从目前状态到下一个状态怎么转换的过程。

更多算法文章：
不含重复项的最长子串
左右括号问题
相亲问题
合并问题

更多精彩内容