序言

现代公钥加密系统中，常用的加密算法除了RSA还有离散对数加密和椭圆曲线加密。这两者原理比较相似，在这里一并介绍。

离散对数问题

我们在中学里学的对数问题是指，

给定正实数 $a$ 和 $a^x$ ，求 $x$ 。也就是计算 $x=\log_a{a^x}$ 。

这是实数域上的对数问题，不是什么难算的东西，随便按一下计算器结果就出来了。

而离散对数问题是指这样的问题：

给定素数 $p$ 和正整数 $g$ ，知道 $g^x\mod p$ 的值，求 $x$

对于符合特定条件的 $p$ 和 $g$ ，这个问题是很难解的，更准确地说，是没有多项式时间的解法。

Diffie–Hellman密钥交换

Diffie–Hellman密钥交换（以下简称DH）是用于双方在可能被窃听环境下安全交换密钥的一种方法。
算法的安全性是由上面提到的离散对数难题保证。

具体算法流程如下：

小红和小明约定 $p$ 和 $g$ 的值

小红生成私钥 $x$ ，计算 $g^x\mod p$ 作为公钥公布出去

小明生成私钥 $y$ ，计算 $g^y\mod p$ 作为公钥公布出去

小红得知 $g^y\mod p$ 后，计算
$s=(g^y\mod p)^x\mod p=(g^y)^x\mod p=g^{xy}\mod p$

小明得到 $g^x\mod p$ 后，计算
$s=(g^x\mod p)^y\mod p=(g^x)^y\mod p=g^{xy}\mod p$

双方都得到了相同的密钥的 $s$ ，交换完毕

上面的流程中， $x$ 和 $y$ 始终由两人自行保管的，第三方窃听得到的只有 $p$ 、 $g$ 、 $g^x\mod p$ 和 $g^y\mod p$ 这几个值。
上面说过，离散对数是很难算的，所以第三方不能由这些信息计算出 $x$ 或 $y$ ，也就没办法计算出密钥 $s$ 了。

椭圆曲线

中学的时候我们学过圆锥曲线，比如椭圆、双曲线和抛物线。因为描述这些曲线的方程都是二次方程，圆锥曲线又被称为二次曲线。而椭圆曲线是则是由三次方程描述的一些曲线。更准确地说，椭圆曲线是由下面的方程描述的曲线：

y^{2} = x^{3} + a x + b 其 中 4 a^{3} + 27 b^{2} \neq 0

$y^2=x^3+ax+b\\ 其中4a^3+27b^2\neq 0$
需要注意的是，椭圆曲线之所以叫“椭圆曲线”，是因为其曲线方程跟利用微积分计算椭圆周长的公式相似。实际上它的图像跟椭圆完全不搭边。

下图是椭圆曲线 $y^2=x^3-x+1$ 的图像
这里写图片描述

椭圆曲线有这样的两个性质：

关于X轴对称

画一条直线跟椭圆曲线相交，它们最多有三个交点

椭圆曲线上的运算

由于椭圆曲线加密进行的运算实际上都是在椭圆曲线上进行的，所以接下来需要定义一些椭圆曲线上的运算。

必须注意的是，这里把这些运算称为“加法”和“乘法”仅仅是方便描述，他们跟平时认知的加法和乘法完全是两码事，完全可以给他们取其它名字（比如”乘法“和”幂运算“等）。

首先定义坐标系中距离X轴无穷远点为椭圆曲线上的一个特殊点，称为0点。
那么此时上述第二条性质可以加强为：过曲线上任意两点（可重合）的直线必定与曲线相交于第三点。
然后定义椭圆曲线上点的加法。设椭圆曲线上有两点，A和B点，那么作过这两点的直线与该曲线相交于第三点（C点），然后关于X轴对称得到D点，则D为这两个点的和，记作 $D=A+B$ 。很明显，D点也在该曲线上。所以椭圆曲线上两点之和也是曲线上的点。

特别地，如果两点重合，则作椭圆曲线在A点处的切线，与曲线相交于第二点（B点），然后关于X轴对称得到C点，则C点为A点与自身的和，记作 $C=A+A$

那么关于这个加法，我们可以得到以下结论：
- $A+B=B+A$
  也就是椭圆曲线上的加法满足交换律。
- $A+0=A$
  因为0点是无穷远点，所以过A点与0点的直线是垂直于X轴的，它与曲线相交于另一点B点，那么B点关于X轴对称的点就是A点，即A点为A点和0点之和。
然后在加法的基础上，定义椭圆曲线上点的乘法。
设 $P$ 是椭圆曲线上的一个点，那么正整数 $k$ 乘以点 $P$ 的结果由下面的式子定义，注意式子中的加法是上面提到的椭圆曲线上点的加法：
$1*P=P$
$2*P=P+P$
$3*P=2*P+P$
…
$k*P=(k-1)*P+P$

这个乘法满足以下性质：

对于任意正整数 $k$ 和 $j$ ，有
$k*(j*P)=(kj)*P=(jk)*P=j*(k*P)$

这个性质在椭圆曲线密钥交换中会利用到。

椭圆曲线上的离散对数问题

定义了基本的加法和乘法运算后，我们可以由此得到椭圆曲线加密依赖的数学难题。

$k$ 为正整数， $P$ 是椭圆曲线上的点（称为基点），已知 $k*P$ 和 $P$ ，计算 $k$

从程序实现的角度来考虑，假设有这么一个函数：

 Point add(Point A, Point B) {...}

函数参数是两个椭圆曲线上的点，返回值是过两个点的直线与椭圆曲线相交的第三个点关于X轴对称的点。
那么按照如下方式调用函数：

Point result = P;
for (int i = 0; i < k - 1; i++)
    result = add(P, result);
sendTo((result, P), others);

如果别人只知道result和P点，是很难求出k的值是多少的。

如果我们改一种记法，把椭圆曲线上点的加法记作乘法，原来的乘法就变成了幂运算，那么上述难题的形式跟离散对数问题应该是一致的。即：

$k$ 为正整数， $P$ 是椭圆曲线上的点，已知 $P^k$ 和 $P$ ，计算 $k=\log_PP^k$ 。

所以这个难题叫椭圆曲线上的离散对数问题。

尽管两者形式一致，但是他们并不等价。实际上这个问题比大整数质因子分解（RSA）和离散对数（DH）难题都要难得多，以致于同样的安全强度下，椭圆曲线加密的密钥比RSA和DH的短不少，这是椭圆曲线加密的一大优势。

有限域上的椭圆曲线

但是密码学中，并不能使用上面介绍的实数域上的椭圆曲线。因为
1. 实数域上的椭圆曲线是连续的，有无限个点，密码学要求有限点。
2. 实数域上的椭圆曲线的运算有误差，不精确。密码学要求精确。

所以我们需要引入有限域上的椭圆曲线。

所谓有限域上的椭圆曲线，简单来说就是满足下面式子要求的曲线（x, y, a, b都是小于素数p的非负整数）：

y^{2} = x^{3} + a x + b \mod p 其 中 4 a^{3} + 27 b^{2} \neq 0 \mod p

$y^2 =x^3+ax+b \mod p\\ 其中4a^3+27b^2\neq 0\mod p$

对比一下原先的椭圆曲线的方程：

y^{2} = x^{3} + a x + b 其 中 4 a^{3} + 27 b^{2} \neq 0

$y^2=x^3+ax+b\\ 其中4a^3+27b^2\neq 0$
可以看到这个只是对原式进行了简单的取模处理而已。实际上RSA和DH中也是基于这种形式的取模运算。

下图是椭圆曲线 $y^2 = x^3 - x + 1$ 对素数97取模后的图像（图片来自参考文献）

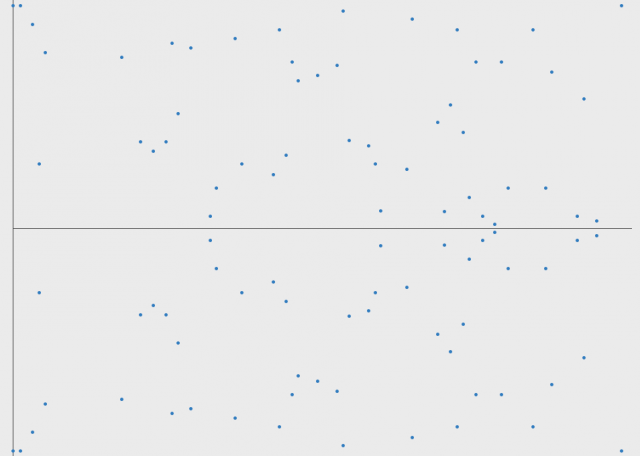
原本连续光滑的曲线变成了离散的点，基本已经面目全非了，但是依然可以看到它是关于某条水平直线（y=97/2）对称的。

而且上面定义的椭圆曲线的加法仍然可用（当然乘法也可以）（图片来自参考文献）。

注意：密码学中有限域上的椭圆曲线一般有两种，一种是定义在以素数p为模的整数域GF(p)，也就是上面介绍的；另一种则是定义在特征为2的伽罗瓦域GF(2^m)上，篇幅所限，这里就不介绍了。

基于椭圆曲线的DH密钥交换（ECDH）

ECDH跟DH的流程基本是一致的。

小红和小明约定使用某条椭圆曲线（包括曲线参数，有限域参数以及基点P等）

小红生成私钥 $x$ ，计算 $x*P$ 作为公钥公布出去

小明生成私钥 $y$ ，计算 $y*P$ 作为公钥公布出去

小红得知 $y*P$ 后，计算
$s=x*(y*P)=xy*P$

小明得到 $x*P$ 后，计算
$s=y*(x*P)=yx*P$

双方都得到了相同的密钥的 $s$ ，交换完毕

由于计算椭圆曲线上的离散对数是很难的，所以第三方没办法在只知道 $x*P$ 和 $y*P$ 的情况下计算出 $x$ 或 $y$ 的值。

实际应用中，我们并不需要关心椭圆曲线的众多参数如何选取（要选对参数对于普通使用者来说并不现实），只要从密码学家们精心挑选的一堆曲线中选择一个就行了。一般来说曲线Curve25519，prime256v1是比较常用的，比特币选择secp256k1则是有自己的考量。

参考文献

浅说椭圆曲线
 A (relatively easy to understand) primer on elliptic curve cryptography
Wikipedia: Elliptic curve
Wikipedia: Elliptic curve cryptography
Bitcoin加密技术之椭圆曲线密码学
 椭圆曲线密码体制

更多精彩内容