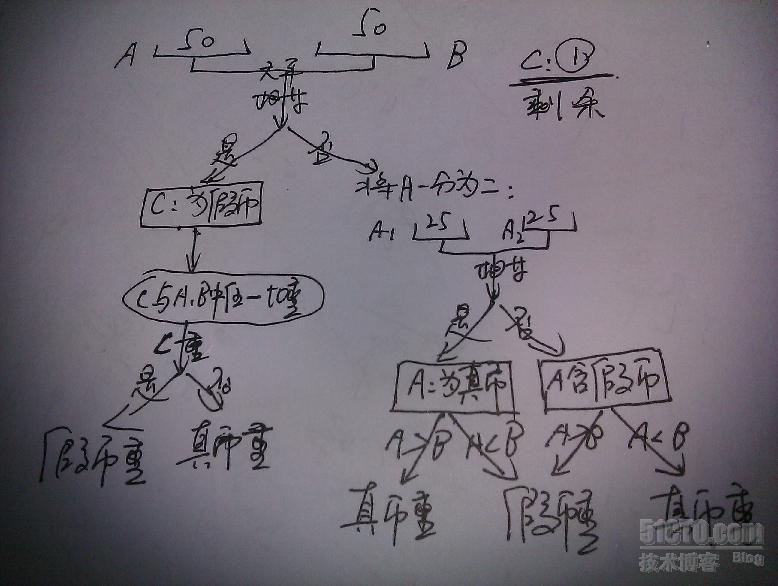
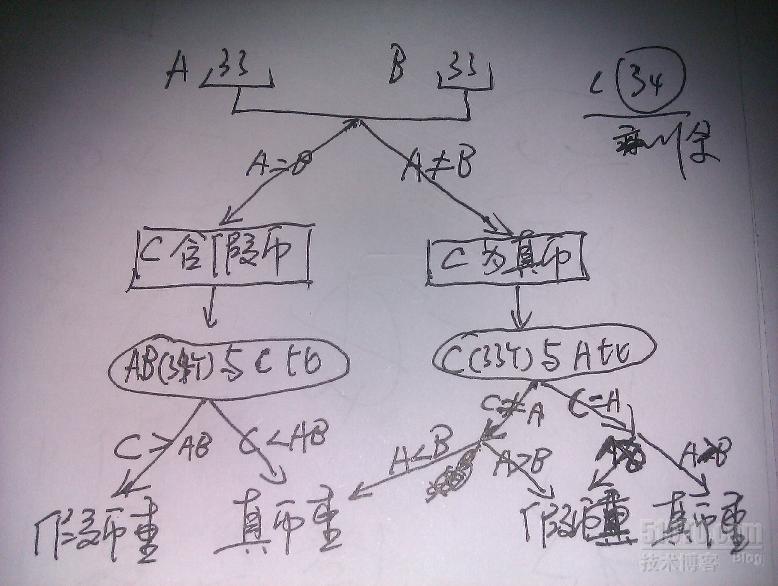
101个硬币中有一个假币,有一个无砝码的天平,称两次,判断假币比真币重还是轻。
把101个硬币平均分成三份,分别是:33,33,35,把两 堆33个放在天平上称。
1、如果平衡,说明这66个都是真的。然后从这两堆共66个中取出35个,与第三堆的35个分别放在天平的左右盘中称,这样,第三堆所在的天平的那一端的轻重就是假币的轻重情况。
1、如果平衡,说明这66个都是真的。然后从这两堆共66个中取出35个,与第三堆的35个分别放在天平的左右盘中称,这样,第三堆所在的天平的那一端的轻重就是假币的轻重情况。
2、如果两 个33放在天平上不平衡,说明第三堆的35个是真的。取下轻的一端的33个,从第三堆中取33个放在上面,如果平衡,说明取下的一堆中有假币,假币比真的轻。如果不平衡,只有一种结果,第三堆与取下的一堆一样,都比那一堆轻,说明假的比真的重。
更多精彩内容